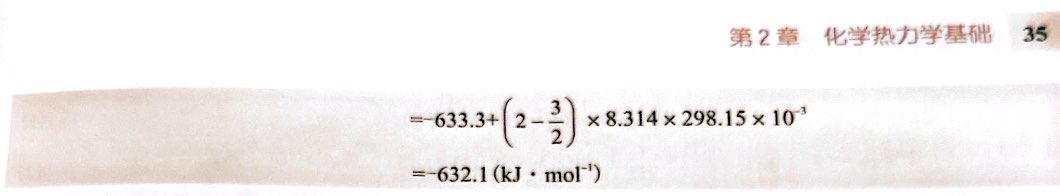第二章 化学热力学基础

基本概念

环境与体系

1. 敞开体系：体系与环境间既有物质交换，又有能力交换
2. 封闭体系：体系与环境间没有物质交换，只有能力交换
3. 孤立体系：体系与环境之间既没有物质交换，也没有能力交换

状态和状态函数

状态：体系存在的某种状态

1. 状态一定：状态函数一定
2. 状态变化：状态函数也随之变化，与路径无关

由$pV=nRT$可知，只需要确定两种性质，就可以确定体系的状态

广度性质和强度性质

1. 广度性质

   在数值上与体系中物质的量成正比，即具有加和性，例如：体积、质量、热力学能、焓、熵、自由能

2. 强度性质

   在数值上与体系中物质的量无关，即不具有加和性，例如：温度、压力、密度、浓度

总结：“量变”可以产生“质变”即为广度性质，由物质本身性质决定即为强度性质

过程和途径

1. 定温过程
2. 定压过程
3. 定容过程
4. 绝热过程
5. 循环过程

热与功

热（heat）与功（work）是交换热量的两种方式

热量从高温物体传递到低温物体，为“热”，用$Q$表示（物理学上的热传导

除此以外的其他方式，为“功”，用$W$表示

按照热力学上的习惯：

• 体系吸热（体系内能量增加），$Q$为正值；体系放热，$Q$为负值
• 体系对环境做功（此时体系内能量减少），$W$为负值；环境对体系做功，$W$为正值

总结：体系内能量增加即为正，体系内能量减少即为负

热力学第一定律

能量守恒定律

体系的热力学改变量为：

$\mathrm{\Delta }U=U_2-U_1=Q+W$

热化学

反应进度

反应进度$\xi$用以表示化学反应进行的程度，给定一化学反应

$aA+dD=gG+hH$

可以表示为

$0=\sum _{B}v(B)·R(B)$

其中，$R(B)$表示的是参与反应的任何物质；$v(B)$即为反应物或者生成物的化学计量数，对反应物来说它是负数（代表消耗），对于生成物来说它是正数（代表生成），化学计量数的量纲为1

误区：其中$B$类似于数学中的$X$，代指反应中的各类反应物和生成物

$v(A)=-a,v(D)=-d,v(G)=g,v(H)=h$

PS：如何理解这些公式呢？其实可以将化学反应式变为数学方程式，即为：

$aA+dD=gG+hH$

$gG+hH-aA-dD=0$

在反应开始时，反应体系中的各物质的量为$n_0(B)$。到反应时刻$t$，反应物的量减少，产物的量增加，各物质的量为$n_t(B)$。反应进度$\xi$的定义为：

其中$\xi$可以理解为摩尔转化率

$\xi =\frac{n_t(B)-n_0(B)}{v_{(}B)}=\frac{\mathrm{\Delta }n(B)}{v_{(}B)}$

用到具体的方程式中，即为：

$\xi =\frac{n_t(A)-n_{0}A}{a}=\frac{\mathrm{\Delta }n(A)}{a}$

化学反应热

热化学中规定：只做体积功的化学反应体系，当反应物的温度和产物的温度相同时，吸收或释放出的热量称为化学反应热

体积功：在热化学中，体积功（也称为膨胀功）是指在化学反应过程中，由于气体体积的变化而做的功。具体来说，当气体在反应中膨胀或压缩时，会对外界做功或被外界做功，这种功称为体积功。

体积功的计算公式：$W=-p\mathrm{\Delta }V$

反应热一般是指反应进度$\xi =1mol$时的热

1. 定容热

   在密闭的容器内进行，反应体系的体积不变，$\mathrm{\Delta }V=0$，体积功$-p\mathrm{\Delta }V$也为零，此时体系的热力学能变化

   $\mathrm{\Delta }U=Q+W=Q_v-p\mathrm{\Delta }V=Q_v$

   其中$Q_v$等于定热容，下标$v$表示体积不变，在只做体积功的条件下，定容反应热等于体系热力学能的改变量，即为$\mathrm{\Delta }Q$

2. 定压热

   只做体积功，在定压条件下进行：

   $\mathrm{\Delta }U=Q+W=Q_p-p\mathrm{\Delta }V$

   故：

   $Q_p=\mathrm{\Delta }U+p\mathrm{\Delta }V=(U_2-U_1)+p(V_2-V_1)=(U_2+p{V}_2)-(U_1+p{V}_1)$

   由于$U、p、V$都为状态函数，所以$U+pV$也是状态函数，热力学中定义一个新的状态函数焓，用符号$H$表示

   $H=U+pV$

   故可得

   $Q_p=(U_2+p{V}_2)-(U_1+p{V}_1)=H_2-H_1$

   在做体积功的条件下，定压反应热等于系统焓的改变量

3. 定压热和定容热的关系

   根据函数焓的定义$H=U+pV$，故体系只做体积功时有：

   $\mathrm{\Delta }H=\mathrm{\Delta }U+\mathrm{\Delta }(pV)$

   由理想气体状态方程：

   $pV=nRT$

   可得

   $\mathrm{\Delta }H=\mathrm{\Delta }U+p\mathrm{\Delta }V=\mathrm{\Delta }U+\mathrm{\Delta }nRT$

   $\mathrm{\Delta }n=\xi \sum v(B,g)=(c\xi +d\xi )-(a\xi +b\xi )$

   对于有气体生成的反应，$pV$不能被忽略

   ${\mathrm{\Delta }}_r{H}_m={\mathrm{\Delta }}_r{U}_m+\sum v(B,g)RT$

   或者

   $Q_{p,m}=Q_{V,m}+\sum v(B,g)RT$

   下标$m$表示反应进度为$\xi =1mol$；$\sum v(B,g)$为反应物和生成物中气相物质的计量数之和

   

   

   热化学方程式

   书写注意事项：

   1. 要注明反应物和产物的状态
   2. 注明反应物和生成物所处的温度和压力
   3. 反应多在定压下完成，用$\mathrm{\Delta }H$表示反应热，负数表示放热，正数表示吸热
   4. ${\mathrm{\Delta }}_r{H}_m^{\mathrm{\Theta }}$的意义是“标准状态下，反应进度$\xi =1mol$时的焓变”
   5. ${\mathrm{\Delta }}_r{H}_m^{\mathrm{\Theta }}$或${\mathrm{\Delta }}_r{H}_m$的单位是$kJ·mo{l}^{-1}$，注意$\mathrm{\Delta }H$代表一个过程的焓变，单位为$J$或$kJ$

赫斯定律

一个反应在定压或定容条件下，不论是一步或者分几步完成，其反应热是相同的

标准摩尔生成焓

由元素的稳定单质生成$1mol$纯化合物时的反应热称为该化合物的标准摩尔生成焓，用${\mathrm{\Delta }}_f{H}_m^{\mathrm{\Theta }}$表示，下标$f$代表生成（formation）

对于任何一个化学反应：

$aA+dD=gG+hH$

其中

${\mathrm{\Delta }}_r{H}_m^{\mathrm{\Theta }}=\sum v(B){\mathrm{\Delta }}_f{H}_m^{\mathrm{\Theta }}(B)$

${\mathrm{\Delta }}_r{H}_m^{\mathrm{\Theta }}=(g{\mathrm{\Delta }}_f{H}_m^{\mathrm{\Theta }}G+h{\mathrm{\Delta }}_f{H}_m^{\mathrm{\Theta }}H-a{\mathrm{\Delta }}_f{H}_m^{\mathrm{\Theta }}A-d{\mathrm{\Delta }}_f{H}_m^{\mathrm{\Theta }}D)$

标准摩尔燃烧焓

在一定温度及标准压力$p^{\mathrm{\Theta }}$下，$1mol$物质完全燃烧时的焓变称为该物质的标准摩尔燃烧焓，用符号${\mathrm{\Delta }}_c{H}_m^{\mathrm{\Theta }}$表示，下标$c$代表燃烧（combustion）

熵

自发过程

1. 自发过程具有方向性
2. 自发过程存在限度
3. 进行自发过程的体系具有做有用功（非体积功）的能力

混乱度和熵

1. 混乱度

   混乱度又称为无序度，它的大小与体系中可能存在的微观状态数目有关

2. 熵

   状态函数，用符号$S$表示

热力学第二定律

说明了自发过程中进行的方向和限度

标准熵

$1mol$纯物质在标准状态下的熵被称为标准摩尔熵，用符号$S_m^{\mathrm{\Theta }}$表示，单位是$J·mo{l}^{-1}·K^{-1}$

化学反应的熵变计算

在标准状态下，化学反应

$aA+dD=gG+hH$

可根据反应物和生成物的标准摩尔熵值求得：

${\mathrm{\Delta }}_r{S}_m^{\mathrm{\Theta }}=\sum v(B)S_m^{\mathrm{\Theta }}(B)$

自由能

自由能

定义：

$G=H-TS$

自由能的变化量可求：

$\mathrm{\Delta }G=G_2-G_1$

可通过自由能来判据反应是否能自发进行：

$\mathrm{\Delta }G<0$ 可自发进行

$\mathrm{\Delta }G=0$ 平衡状态

$\mathrm{\Delta }G>0$ 非自发过程，其逆反应过程可自发进行

标准摩尔生成自由能

由稳定单质生成$1mol$物质时自由能的变化就是该物质的标准摩尔生成自由能，用符号${\mathrm{\Delta }}_f{G}_m^{\mathrm{\Theta }}$表示，其单位是$kJ·mo{l}^{-1}$

在标准状态下，化学反应的吉布斯自由能改变量

${\mathrm{\Delta }}_r{G}_m^{\mathrm{\Theta }}=\sum v(B){\mathrm{\Delta }}_f{G}_m^{\mathrm{\Theta }}(B)$

吉布斯-亥姆霍兹方程

根据自由能定义$G=H-TS$，在定温条件下

$\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S$

自由能的改变是$\mathrm{\Delta }G$总和了$\mathrm{\Delta }H$和$\mathrm{\Delta }S$后的结果，可写为：

${\mathrm{\Delta }}_r{G}_m^{\mathrm{\Theta }}={\mathrm{\Delta }}_r{H}_m^{\mathrm{\Theta }}-T{\mathrm{\Delta }}_r{S}_m^{\mathrm{\Theta }}$